 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
| image = | frequencyFiltering3dImg (inImg3d,frequencyBandPassFilterType,cutoffFrequency,inStdDev) |
| image = | frequencyFiltering3dImg (inImg3d,frequencyBandPassFilterType,cutoffFrequency,inStdDev,theta,thetaRange,phi,phiRange) |
Filters a 3d image in Fourier domain by selecting a frequency range.
This algorithm applies a band-pass filter to the input image in the frequency domain. Such an approach is very powerful since a convolution in the spatial domain becomes a voxelwise multiplication in the Fourier domain. Hence, it is computationnally faster than a spatial filtering, in particular for large kernel sizes and 3d data. Moreover, it is possible to design a filter in order to fit a determined frequency range.
The steps of the algorithm are:
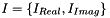 , the disctrete Fourier transform of the input image,
, the disctrete Fourier transform of the input image,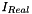 and
and 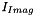 by its related filter coefficient,
by its related filter coefficient,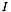 ,
,As for the 2d version of this algorithm, the user can specify two different band-pass filters :
![\[ F(f) = e^{-\frac{ \left( f - f_0 \right)^2}{2 \sigma^2}} \]](form_512.png)
![\[ F(f) = e^{-\frac{ \left( \log \left( f / f_0 \right) \right)^2}{2 \left( \log \left( \sigma / f_0 \right) \right)^2}} \]](form_513.png)
where 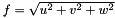 ,
, 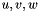 being respectively the frequencies along the image axes (see Band-pass frequency filtering 2d for more details about these filters).
being respectively the frequencies along the image axes (see Band-pass frequency filtering 2d for more details about these filters).
In some images, it may be interesting to isolate a texture with a specific 3d orientation. For this reason, the algorithm allows to specify orientations theta and phi, as well as their ranges thetaRange and phiRange which will mask the filtered spectrum and keep only the information in the desired direction range, in degrees.
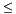 theta
theta 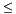 180°, -180°
180°, -180° 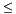 phi
phi 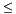 180° and 0° < thetaRange, phiRange
180° and 0° < thetaRange, phiRange 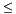 180°. If not, the default values are theta = phi = 0° and thetaRange = phiRange = 180° (i.e. select all the orientations). Moreover, because of the the definition of theta (see Points and vectors 3d representation), only values between 0° and 180° are posible, hence the range [theta-thetaRange, theta+thetaRange] is saturated if it exceeds these limits.
180°. If not, the default values are theta = phi = 0° and thetaRange = phiRange = 180° (i.e. select all the orientations). Moreover, because of the the definition of theta (see Points and vectors 3d representation), only values between 0° and 180° are posible, hence the range [theta-thetaRange, theta+thetaRange] is saturated if it exceeds these limits.See Band-pass frequency filtering 2d for a 2d example of band-pass filtering and Points and vectors 3d representation for more details about 3d trigonometry convention.