 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
| image = | convolution2dImg (inImg,inKnlXY,inNormalize) |
| image = | convolution2dImg (inImg,inKnlXY,inNormalize,inOptConvolBorder2d) |
Compute convolution of an input 2d image with a kernel.
See Kernels for a detailled documentation of kernels creation and management tools.
Given an input 2d kernel :
![\[ InKnlXY(o_{x}, o_{y}), \forall \left\{o_{x}, o_{y}\right\}\in \left [-\dfrac{n^{-}_{x}}{2},\dfrac{n^{+}_{x}}{2}\right ]\times\left [-\dfrac{n^{-}_{y}}{2},\dfrac{n^{+}_{y}}{2}\right ] \]](form_441.png)
Where :
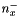 defines "negative" part of kernel elements along x axis (elements before central element)
defines "negative" part of kernel elements along x axis (elements before central element)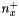 defines "positive" part of kernel elements along x axis (elements after central element)
defines "positive" part of kernel elements along x axis (elements after central element)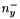 defines "negative" part of kernel elements along y axis (elements before central element)
defines "negative" part of kernel elements along y axis (elements before central element)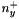 defines "positive" part of kernel elements along y axis (elements after central element)
defines "positive" part of kernel elements along y axis (elements after central element)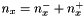 defines kernel size along x axis
defines kernel size along x axis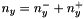 defines kernel size along y axis
defines kernel size along y axisExample of square kernel with 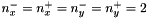 (unsharp making kernel) :
(unsharp making kernel) :
![\[ InKnlXY = -\dfrac{1}{256} \begin{bmatrix} 1 & 4 & 6 & 4 & 1 \\ 4 & 16 & 24 & 16 & 4 \\ 6 & 24 & -476 & 24 & 6 \\ 4 & 16 & 24 & 16 & 4 \\ 1 & 4 & 6 & 4 & 1 \end{bmatrix} \]](form_449.png)
Example of square kernel with 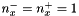 and
and 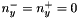 (linear box filter kernel) :
(linear box filter kernel) :
![\[ InKnlXY = \dfrac{1}{3} \begin{bmatrix} 1 & 1 & 1 \end{bmatrix} \]](form_452.png)
On output image values are given by:
![\[ OutImg[x, y] = \sum_{o_{y}=-\dfrac{n_{y}}{2}}^{\dfrac{n_{y}}{2}}{\sum_{o_{x}=-\dfrac{n_{x}}{2}}^{\dfrac{n_{x}}{2}}{InImg[x+o_{x}, y+o_{y}] \times InKnlXY[o_{x}, o_{y}]}} \]](form_453.png)
Input kernel coefficients can be normalized during processing if 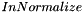 value is set to
value is set to 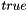 . In this case previous formula is modified into :
. In this case previous formula is modified into :
![\[ OutImg[x, y] = \dfrac{1}{K}\sum_{o_{y}=-\dfrac{n_{y}}{2}}^{\dfrac{n_{y}}{2}}{\sum_{o_{x}=-\dfrac{n_{x}}{2}}^{\dfrac{n_{x}}{2}}{InImg[x+o_{x}, y+o_{y}] \times InKnlXY[o_{x}, o_{y}]}} \]](form_456.png)
with :
![\[ K = \sum_{o_{y}=-\dfrac{n_{y}}{2}}^{\dfrac{n_{y}}{2}}{\sum_{o_{x}=-\dfrac{n_{x}}{2}}^{\dfrac{n_{x}}{2}}{InKnlXY[o_{x}, o_{y}]}} \]](form_457.png)
Case of 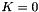 is handled forcing its value to
is handled forcing its value to 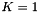 to avoid null division.
to avoid null division.
Neighborhood border policy is controlled by 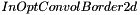 parameter. This parameter allows to control starting and ending rows/columns provided data during processing (see Border policy for more details).
parameter. This parameter allows to control starting and ending rows/columns provided data during processing (see Border policy for more details).
Here is an example of a normalized convolution operation applied to an 8-bits grey levels input image with input kernel given by :
![\[ InKnlXY = \dfrac{1}{49}\left( \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix}^T \times \begin{bmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1 \end{bmatrix} \right) \]](form_460.png)
