image =	deepFlow2dImg (inImg1,inImg2)
image =	deepFlow2dImg (inImg1,inImg2,params)

Detailed Description

Computes a dense optical flow occurred between two input images.

This algorithm computes the optical flow between 2 input images using the deep flow algorithm [1].

1- Optical flow presentation

The optical flow is the apparent motion of objects that occurred between two images. It relies on the assumption of intensity conservation and can be expressed as:

$I[x, y, t] = I[x+dx, y+dy, t+dt]$

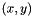where $I[x, y, t]$ is a pixel $(x, y)$ in the image at the time 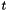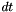$t$ , $dt$ is the time between two frames and 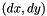$(dx, dy)$ is the displacement that occurred during $dt$ .

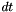Assuming the displacement is small enough, this equation can be approximated by a first order Taylor expansion:

$I(x+dx, y+dy, t+dt) = I(x, y, t) + \frac{\partial I}{\partial x} dx + \frac{\partial I}{\partial y} dy + \frac{\partial I}{\partial t} dt$

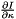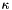where $\frac{\partial I}{\partial \kappa}$ is the partial derivative of the image along the dimension $\kappa$ .

Dividing by 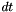$dt$ and using the intensity conservation assumption, the equation becomes:

$\frac{\partial I}{\partial x} u + \frac{\partial I}{\partial y} v + \frac{\partial I}{\partial t} = 0$

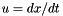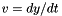where $u = dx/dt$ and $v = dy/dt$ .

This equation can not be directly solved since we only have one equation for 2 unknowns to estimate.

2- DeepFlow description

The DeepFlow is one of the several technics to solve the equation above. It is a variational method that integrates a multiscale approach to overcome the limit of small displacement assumption.

In this algorithm, solving the optical flow problem consists in minimizing the energy 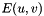$E(u, v)$ defined as:

$E(u, v) = \int_\Omega E_D + \alpha E_S + \beta E_M dx$

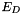where $E_D$ is the energy of the data term, ensuring that the intensities stay close, 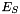$E_S$ represents the smoothing term, ensuring a local consistency of the flow gradient and 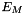$E_M$ is a matching term, ensuring that the estimated flow is close to the input a priori flow. In practice, this implementation stays to more standard variation model and ignores the mathcing term [2]. The equation becomes:

$E(u, v) = \int_\Omega E_D + \alpha E_S dx$

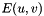$E(u, v)$ is iteratively minimized using a Successive Over-relaxation (SOR) approach, taking the flow estimated at the scale 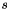$s$ as initialization of the estimation at the scale $s+1$ .

3- Parameters description

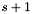The algorithm takes the following parameters:

the two input images (can not be sequence images)
an optional flow, used as initial flow if provided,
NbMaxLayers : the number of scales. The algorithm ensures that the downscale image is not too small. Consequently, the actual number of scales may be lower than the value provided.
DownscaleFactor : the scaling factor between two consecutive levels (must be < 1)
FixedPointIterations How many iterations on each level of the pyramid
SorIterations : nomber of iterations of Succesive Over-Relaxation (solver)
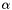$\alpha$ : the smoothness weight
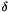$\delta$ : the color constancy weight (see [1] for more details)
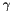$\gamma$ : the gradient constancy weight
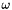$\omega$ : Relaxation factor in SOR

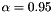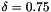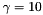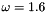The figure below presents and example of flow estimation. A random and smooth deformation field was applied to the image of lena. The deep flow was calculated with the folowing parameters: 200 layers (maximum), downscale factor = 0.95, 5 fixed point iterations, 25 SOR iterations, $\alpha=0.95$ , $\delta=0.75$ , $\gamma=10$ , $\omega=1.6$ :

[1] Philippe Weinzaepfel, Jerome Revaud, Zaid Harchaoui, and Cordelia Schmid. Deepflow: Large displacement optical flow with deep matching. In Computer Vision (ICCV), 2013 IEEE International Conference on, pages 1385�1392. IEEE, 2013.

[2] Brox, T., Bruhn, A., Papenberg, N., Weickert, J. (2004). High Accuracy Optical Flow Estimation Based on a Theory for Warping. In: Pajdla, T., Matas, J. (eds) Computer Vision - ECCV 2004. ECCV 2004.

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLRegistration as registration

Code Example

    # Set up the parameters
    params = PyIPSDK.createDeepFlowParams(nbLayers, downscaleFactor, fixedPointIterations, sorIterations, alpha, delta, gamma, omega)
    
    # Compute the flow
    outImg = registration.deepFlow2dImg(inImg1, inImg2, params)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLRegistration/Processor/DeepFlow2dImg/DeepFlow2dImg.h>

Code Example

            // Setup the parameters
            DeepFlowParamsPtr pParams = createDeepFlowParams(nbLevels, downscaleFactor,
                                                             fixedPointIterations, sorIterations,
                                                             alpha, delta, gamma, omega);
            // Process the operation
            ImagePtr pOutImg = deepFlow2dImg(pInImg1, pInImg2, pParams);