xGradImg,yGradImg,zGradImg =	gaussianGradient3dImg (inImg3d,inStdDev)
xGradImg,yGradImg,zGradImg =	gaussianGradient3dImg (inImg3d,inStdDevX,inStdDevY,inStdDevZ,inOptGradientGaussianCoverage)
image =	gaussianXGradient3dImg (inImg3d,inStdDev)
image =	gaussianYGradient3dImg (inImg3d,inStdDev)
image =	gaussianZGradient3dImg (inImg3d,inStdDev)

Detailed Description

Compute X, Y and Z gradients of an input image convolving it with 3d Gaussian kernels.

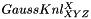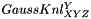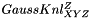Used Gaussian kernels $GaussKnl^{X}_{XYZ}$ , $GaussKnl^{Y}_{XYZ}$ and $GaussKnl^{Z}_{XYZ}$ coefficients are defined as follow :

$GaussKnl^{X}_{XYZ}[o_x, o_y, o_z] = -\dfrac{o_x}{(2\pi)^\frac{3}{2}\sigma^5}e^{-\dfrac{o_x^2+o_y^2+o_z^2}{2\sigma^2}}$

$GaussKnl^{Y}_{XYZ}[o_x, o_y, o_z] = -\dfrac{o_y}{(2\pi)^\frac{3}{2}\sigma^5}e^{-\dfrac{o_x^2+o_y^2+o_z^2}{2\sigma^2}}$

$GaussKnl^{Z}_{XYZ}[o_x, o_y, o_z] = -\dfrac{o_z}{(2\pi)^\frac{3}{2}\sigma^5}e^{-\dfrac{o_x^2+o_y^2+o_z^2}{2\sigma^2}}$

where :

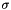$\sigma$ is defined by InStdDev attribute

Size $[n_x, n_y, n_z]$ of this finite kernel is controlled by InOptGradientGaussianCoverage attribute.
This parameter defined the minimum distribution spread ratio which should be reach regards to an infinite Gaussian distribution.
We define for example 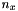$n_x$ such that :

$n_x = \max(MinHalfKernelSize, \min(\{n\}\in \mathbb{N}^+) / \sum_{o_x=-\dfrac{n_x}{2}}^{\dfrac{n_x}{2}}{GaussKnl_X[o_x]}>= GaussianRatio \times \sum_{o_x=-\infty}^{+\infty}{GaussKnl_X[o_x]})$

where :

$GaussKnl_X[o_x] = \dfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{o_x^2}{2\sigma^2}}$

On output image values are given by:

$OutOptGradXImg3d[x, y, z] = \sum_{o_z=-\dfrac{n_z}{2}}^{\dfrac{n_z}{2}}{\sum_{o_y=-\dfrac{n_y}{2}}^{\dfrac{n_y}{2}}{\sum_{o_x=-\dfrac{n_x}{2}}^{\dfrac{n_x}{2}}{InImg3d[x+o_x, y+o_y, z+o_z] \times GaussKnl^{X}_{XYZ}[o_x, o_y, o_z]}}}$

$OutOptGradYImg3d[x, y, z] = \sum_{o_z=-\dfrac{n_z}{2}}^{\dfrac{n_z}{2}}{\sum_{o_y=-\dfrac{n_y}{2}}^{\dfrac{n_y}{2}}{\sum_{o_x=-\dfrac{n_x}{2}}^{\dfrac{n_x}{2}}{InImg3d[x+o_x, y+o_y, z+o_z] \times GaussKnl^{Y}_{XYZ}[o_x, o_y, o_z]}}}$

$OutOptGradZImg3d[x, y, z] = \sum_{o_z=-\dfrac{n_z}{2}}^{\dfrac{n_z}{2}}{\sum_{o_y=-\dfrac{n_y}{2}}^{\dfrac{n_y}{2}}{\sum_{o_x=-\dfrac{n_x}{2}}^{\dfrac{n_x}{2}}{InImg3d[x+o_x, y+o_y, z+o_z] \times GaussKnl^{Z}_{XYZ}[o_x, o_y, o_z]}}}$

A detailled analysis of this filter has been done in J. Canny (1986) "A computational approach to edge detection", IEEE Trans. Pattern Analysis and Machine Intelligence, vol 8, pages 679-714.

Output images OutOptGradXImg3d, OutOptGradYImg3d and OutOptGradZImg3d are optional (at least one must be provided). Input and output images must have same size.

Here is an example of a Gaussian gradient operation applied to an 8-bits grey levels input image (with 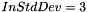$InStdDev=3$ ):

See also: http://en.wikipedia.org/wiki/Edge_detection#cite_note-8

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLFiltering as filter

Code Example

    # opening of input images
    inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
    
    # gaussian gradient filter 3d computation
    outGxImg,  outGyImg,  outGzImg = filter.gaussianGradient3dImg(inImg, 1.5)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLFiltering/Processor/GaussianGradient3dImg/GaussianGradient3dImg.h>

Code Example

    // opening input image
    ImagePtr pInImg3d = loadTiffImageFile(inputImgPath, eTiffDirectoryMode::eTDM_Volume);
        
    // compute gaussian gradient on input image
    GradientXYZImg gradientXYZ = gaussianGradient3dImg(pInImg3d, inStdDev, inStdDev, inStdDev, createGaussianCoverage(inOptGaussianRatio, minHalfKernelSize));