hxxImg,hxyImg,hyyImg =	gaussianHessian2dImg (inImg,inStdDev)
hxxImg,hxyImg,hyyImg =	gaussianHessian2dImg (inImg,inStdDevX,inStdDevY,inOptHessianGaussianCoverage)

Detailed Description

Gaussian filter used to compute Hessian on a 2d image.

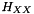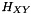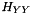Used Gaussian Hessian kernel $H_{XX}$ , $H_{XY}$ and $H_{YY}$ coefficients are defined as follow :

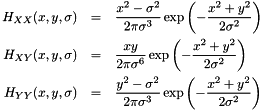
$\begin{eqnarray*} H_{XX}(x, y, \sigma) & = & \frac{x^2 - \sigma^2}{2\pi \sigma^3} \exp \left( - \frac{x^2 + y^2}{2 \sigma^2} \right)\\ H_{XY}(x, y, \sigma) & = & \frac{xy}{2\pi \sigma^6} \exp \left( - \frac{x^2 + y^2}{2 \sigma^2} \right)\\ H_{YY}(x, y, \sigma) & = & \frac{y^2 - \sigma^2}{2\pi \sigma^3} \exp \left( - \frac{x^2 + y^2}{2 \sigma^2} \right) \end{eqnarray*}$

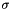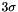where $\sigma$ is defined by InStdDev attribute. The size $[n_x, n_y]$ of this finite kernel is controlled by InOptGradientGaussianCoverage attribute and is at least $3\sigma$ in each direction.
This parameter defined the minimum distribution spread ratio which should be reach regards to an infinite Gaussian distribution. We define for example 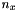$n_x$ such that :

$n_x = \max(MinHalfKernelSize, \min(\{n\}\in \mathbb{N}^+) / \sum_{o_x=-\frac{n_x}{2}}^{\frac{n_x}{2}}{GaussKnl_X[o_x]} \geq GaussianRatio \times \sum_{o_x=-\infty}^{+\infty}{GaussKnl_X[o_x]})$

where :

$GaussKnl_X[o_x] = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{o_x^2}{2\sigma^2}}$

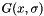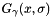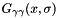The algorithm uses a separable approach in order to reduce the number of operations. Let's consider the three 1d filters $G(x, \sigma)$ , $G_{\gamma}(x, \sigma)$ and $G_{\gamma \gamma}(x, \sigma)$ along the x-axis:

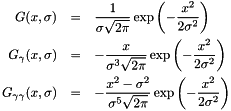
$\begin{eqnarray*} G(x, \sigma) & = & \frac{1}{\sigma \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right)\\ G_{\gamma}(x, \sigma) & = & -\frac{x}{\sigma^3 \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right)\\ G_{\gamma \gamma}(x, \sigma) & = & -\frac{x^2-\sigma^2}{\sigma^5 \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right) \end{eqnarray*}$

Where 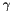$\gamma$ correspond to the x- or y-direction. The filters are transposed to get the filter along the y-axis.

For a given standard deviation 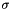$\sigma$ , the output images OutHxxImg, OutHyyImg and OutHxyImg are calculated as follows:

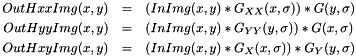
$\begin{eqnarray*} OutHxxImg(x, y) & = & \left( InImg(x, y) * G_{XX}(x, \sigma) \right) * G(y, \sigma)\\ OutHyyImg(x, y) & = & \left( InImg(x, y) * G_{YY}(y, \sigma) \right) * G(x, \sigma)\\ OutHxyImg(x, y) & = & \left( InImg(x, y) * G_{ X }(x, \sigma) \right) * G_{Y}(y, \sigma) \end{eqnarray*}$

Where $ * $ is the convolution operator.

Here is an example of a Gaussian Hessian operation applied to an 8-bits grey levels input image (with 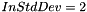$InStdDev=2$ ):

See also: https://en.wikipedia.org/wiki/Hessian_matrix

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLFiltering as filter

Code Example

    # opening of input images
    inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
    
    # gaussian gradient filter 2d computation
    outHxxImg, outHxyImg, outHyyImg = filter.gaussianHessian2dImg(inImg, 1.5)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLFiltering/Processor/GaussianHessian2dImg/GaussianHessian2dImg.h>

Code Example

    // opening input image
    ImagePtr pInImg = loadTiffImageFile(inputImgPath);
        
    // compute gaussian gradient on input image
    HessianXYImg hessianXY = gaussianHessian2dImg(pInImg, inStdDev, inStdDev, createGaussianCoverage(inOptGaussianRatio, minHalfKernelSize));