hxxImg,hxyImg,hxzImg,hyyImg,hyzImg,hzzImg =	gaussianHessian3dImg (inImg,inStdDev)
hxxImg,hxyImg,hxzImg,hyyImg,hyzImg,hzzImg =	gaussianHessian3dImg (inImg,inStdDevX,inStdDevY,inStdDevZ,inOptHessianGaussianCoverage)

Detailed Description

Gaussian filter used to compute Hessian on a 3d image.

The GaussianHessian3dImg algorithm uses separable Gaussian derivarive and smoothing filters to compute the Hessian matrix coefficient on each voxels.

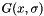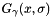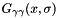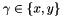Let's consider the three 1d filters $G(x, \sigma)$ , $G_{\gamma}(x, \sigma)$ and $G_{\gamma \gamma}(x, \sigma)$ along the direction $\gamma \in \left\{ x, y \right\}$ :

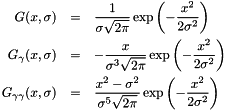
$\begin{eqnarray*} G(x, \sigma) & = & \frac{1}{\sigma \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right)\\ G_{\gamma}(x, \sigma) & = & -\frac{x}{\sigma^3 \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right)\\ G_{\gamma \gamma}(x, \sigma) & = & \frac{x^2-\sigma^2}{\sigma^5 \sqrt{2 \pi}} \exp \left( - \frac{x^2}{2 \sigma^2} \right) \end{eqnarray*}$

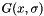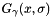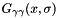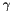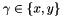$G(x, \sigma)$ is a smoothing function , $G_{\gamma}(x, \sigma)$ is the first order gaussian derivative and $G_{\gamma \gamma}(x, \sigma)$ is the second order Gaussian derivative along the directon $\gamma$ , $\gamma \in \left\{ x, y \right\}$ .

The kernels used for these filters have a size of 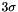$3\sigma$ . The Hessian coefficients are caultulated by a combination of these kernels:

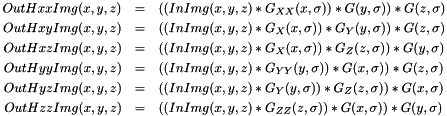
$\begin{eqnarray*} OutHxxImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{XX}(x, \sigma) \right) * G(y, \sigma) \right) * G(z, \sigma)\\ OutHxyImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{X}(x, \sigma) \right) * G_{Y}(y, \sigma) \right) * G(z, \sigma)\\ OutHxzImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{X}(x, \sigma) \right) * G_{Z}(z, \sigma) \right) * G(y, \sigma)\\ OutHyyImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{YY}(y, \sigma) \right) * G(x, \sigma) \right) * G(z, \sigma)\\ OutHyzImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{Y}(y, \sigma) \right) * G_{Z}(z, \sigma) \right) * G(x, \sigma)\\ OutHzzImg(x, y, z) & = & \left( \left( InImg(x, y, z) * G_{ZZ}(z, \sigma) \right) * G(x, \sigma) \right) * G(y, \sigma) \end{eqnarray*}$

See Gaussian Hessian 2d for an illustration of a 2d Gaussian Hessian result.

See also: https://en.wikipedia.org/wiki/Hessian_matrix

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLFiltering as filter

Code Example

    # opening of input images
    inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
    
    # gaussian gradient filter 2d computation
    outHxxImg, outHxyImg, outHxzImg, outHyyImg, outHyzImg, outHzzImg = filter.gaussianHessian3dImg(inImg, 1.5)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLFiltering/Processor/GaussianHessian3dImg/GaussianHessian3dImg.h>

Code Example

    // opening input image
    ImagePtr pInImg3d = loadTiffImageFile(inputImgPath, eTiffDirectoryMode::eTDM_Volume);
        
    // compute gaussian gradient on input image
    HessianXYZImg hessianXYZ = gaussianHessian3dImg(pInImg3d, inStdDev, inStdDev, inStdDev, createGaussianCoverage(inOptGaussianRatio, minHalfKernelSize));