 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
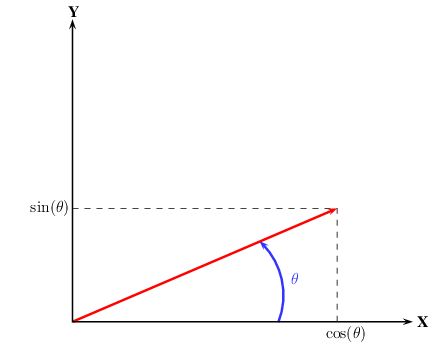
Points 2d can be represented alternatively using carthesian or polar coordinates. These two representation are linked by the following formula :
![\[ P = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \rho\cos(\theta) \\ \rho\sin(\theta) \end{pmatrix} \]](IPSDKCore_form_0.png)
where :
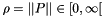 is the L2 norm (euclidian norm) of
is the L2 norm (euclidian norm) of 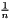
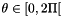 is the azimuth
is the azimuth 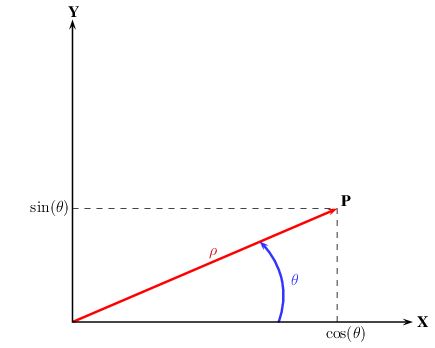
Lines 2d can be represented using polar coordinates.
![\[ \cos{\theta} \times x + \sin{\theta} \times y = \rho \]](IPSDKCore_form_4.png)
where :
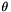 is the angle (in radian) between line normal and axis of abscissas
is the angle (in radian) between line normal and axis of abscissas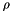 is the distance from line to origin
is the distance from line to origin 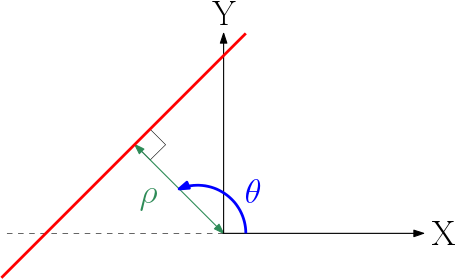
Rotations 2d are expressed with respect to direct referential orientation.
A 2d rotation with angle 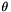 can be represented as follow :
can be represented as follow :
Given a point 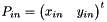 , its transformed is obtain by :
, its transformed is obtain by :
![\[ \begin{pmatrix} x_{out} \\ y_{out} \end{pmatrix} = \begin{pmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{pmatrix} \begin{pmatrix} x_{in} \\ y_{in} \end{pmatrix} \]](IPSDKCore_form_8.png)
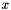 axis
axis 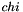 is transformed in
is transformed in 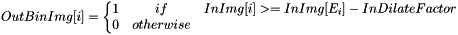 .
. 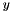 axis
axis 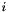 is transformed in
is transformed in 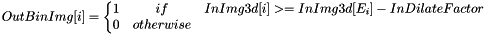 .
.Points 3d can be represented alternatively using carthesian or spherical coordinates. These two representation are linked by the following formula :
![\[ P = \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} \rho\sin(\theta)\cos(\phi) \\ \rho\sin(\theta)\sin(\phi) \\ \rho\cos(\theta) \end{pmatrix} \]](IPSDKCore_form_15.png)
where :
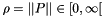 is the L2 norm (euclidian norm) of
is the L2 norm (euclidian norm) of 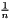
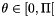 is the inclination
is the inclination![$\phi \in [0, 2\Pi]$](IPSDKCore_form_17.png) is the azimuth
is the azimuth 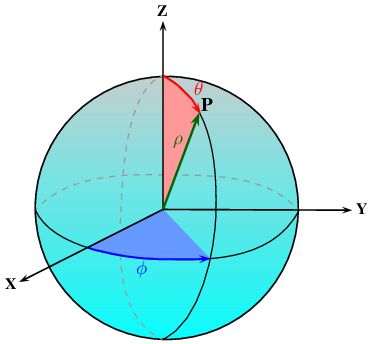
Plans 3d can be represented using spherical coordinates.
![\[ \vec{\eta} = \begin{pmatrix} \sin(\theta)\cos(\phi) \\ \sin(\theta)\sin(\phi) \\ \cos(\theta) \end{pmatrix} \]](IPSDKCore_form_18.png)
where :
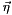 is the orthogonal direction to plan.
is the orthogonal direction to plan.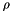 is the distance from plan to origin
is the distance from plan to origin 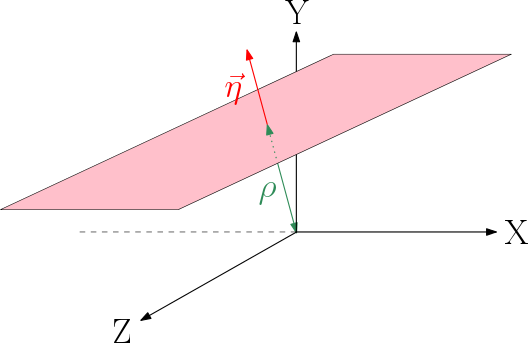
Rotations 3d are expressed with respect to direct referential orientation.
These rotations can be expressed as the product of three elemental rotations using Euler notations :
![\[R(\chi, \beta, \alpha) = R_z(\chi) \times R_y(\beta) \times R_x(\alpha)\]](IPSDKCore_form_20.png)
where :
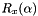 is a rotation around
is a rotation around 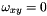 axis
axis 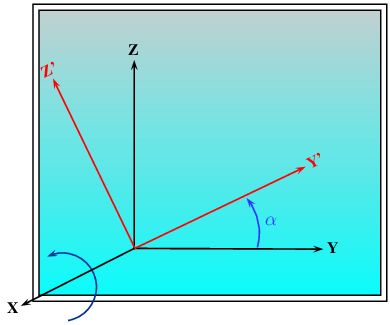
![\[ R_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha) & -sin(\alpha) \\ 0 & sin(\alpha) & cos(\alpha) \\ \end{pmatrix} \]](IPSDKCore_form_23.png)
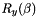 is a rotation around
is a rotation around  axis
axis 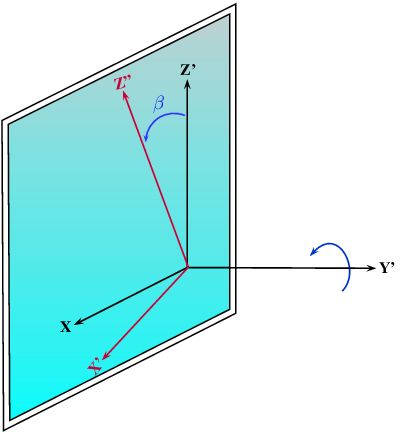
![\[ R_y(\beta) = \begin{pmatrix} cos(\beta) & 0 & sin(\beta) \\ 0 & 1 & 0 \\ -sin(\beta) & 0 & cos(\beta) \\ \end{pmatrix} \]](IPSDKCore_form_26.png)
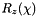 is a rotation around
is a rotation around  axis
axis 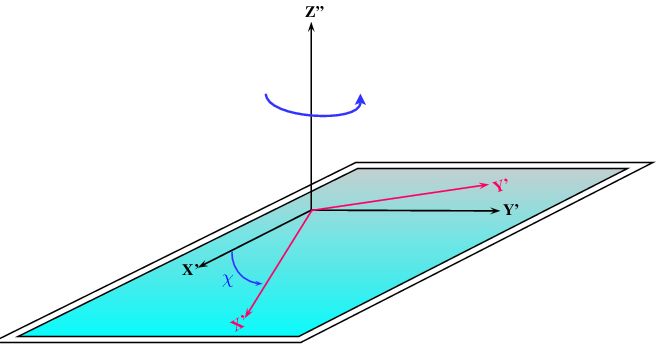
![\[ R_z(\chi) = \begin{pmatrix} cos(\chi) & -sin(\chi) & 0 \\ sin(\chi) & cos(\chi) & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \]](IPSDKCore_form_29.png)
Full rotation matrix is given by :
![\[ R(\chi, \beta, \alpha) = R_z(\chi) \times R_y(\beta) \times R_x(\alpha) = \begin{pmatrix} cos(\chi)cos(\beta) & cos(\chi)sin(\beta)sin(\alpha) - sin(\chi)cos(\alpha) & cos(\chi)sin(\beta)cos(\alpha) + sin(\chi)sin(\alpha) \\ sin(\chi)cos(\beta) & sin(\chi)sin(\beta)sin(\alpha) + cos(\chi)cos(\alpha) & sin(\chi)sin(\beta)cos(\alpha) - cos(\chi)sin(\alpha) \\ -sin(\beta) & cos(\beta)sin(\alpha) & cos(\beta)cos(\alpha) \\ \end{pmatrix} \]](IPSDKCore_form_30.png)