Measure allowing to compute the second order moment ponderated by the gray level of each pixel for shape.
The GreyInertia measurement computes the second order central moment for each shape, ponderated by the voxels intensities, thanks to the inertia matrix 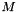 .
.
![\[ M = \begin{bmatrix} m_{xx} & m_{xy} & m_{xz} \\ m_{yx} & m_{yy} & m_{yz} \\ m_{zx} & m_{zy} & m_{zz} \end{bmatrix} \]](form_1091.png)
Whose the components are computed as follows :
![\[ \begin{array}{r c l} m_{xx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right)^2 I(x, y, z)} \\ m_{xy} = m_{yx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right) \left(y - \bar{y} \right) I(x, y, z)} \\ m_{xz} = m_{zx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right) \left(z - \bar{z} \right) I(x, y, z)} \\ m_{yy} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(y - \bar{y} \right)^2 I(x, y, z)}\\ m_{yz} = m_{zy} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(y - \bar{y} \right) \left(z - \bar{z} \right) I(x, y, z)} \\ m_{zz} = m_{zz} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(z - \bar{z} \right) \left(z - \bar{z} \right) I(x, y, z)} \end{array} \]](form_1092.png)
Where 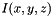 is the image intensity at the position
is the image intensity at the position 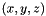 ,
, 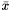 ,
, 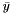 and
and 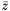 are the grey barycenter coordinates (see GreyBarycenter) and
are the grey barycenter coordinates (see GreyBarycenter) and 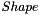 is the voxel collection of the current shape.
is the voxel collection of the current shape.
From these composents, three descriptors are extracted in 2d : the minimum and maximum eigen values of 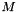 (
( 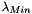 and
and 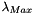 ) and the shape orientation
) and the shape orientation 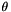 .
.
These features are calculated as follows :
![\[ \begin{array}{r c l} \delta & = & \sqrt{(m_{xx} - m_{yy}) (m_{xx} - m_{yy}) + 4 m_{xy} m_{xy}} \\ \lambda_{Max} & = & \frac{1}{2} \left( m_{xx} + m_{yy} + \delta \right) \\ \lambda_{Min} & = & \frac{1}{2} \left( m_{xx} + m_{yy} - \delta \right) \\ \theta & = & \tan^{-1} \left( \frac{\lambda_{Max} - m_{xx}}{m_{xy}} \right) \end{array} \]](form_1100.png)
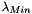 and
and 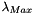 are proportional to the squared length of the eigenvector axes, represented by green arrows in the figure below.
are proportional to the squared length of the eigenvector axes, represented by green arrows in the figure below.
In 3d case, other features are available. They are calculated as follows :
![\[ \begin{array}{r c l} q & = & \frac{m_{xx} + m_{yy} + m_{zz}}{3} \\ p & = & \sqrt{\frac{(m_{xx} - q)^2 + (m_{yy} - q)^2 + (m_{zz} - q)^2 + 2 (m_{xy}^2 + m_{xz}^2 + m_{yz}^2)}{6}} \\ \lambda_{Max} & = & q + 2 p \cos(\phi + 2 \pi / 3) \\ \lambda_{Inter} & = & q + 2 p \cos(\phi - 2 \pi / 3) \\ \lambda_{Min} & = & q + 2 p \cos(\phi) \end{array} \]](form_1101.png)
Where :
![\[ \phi = \begin{cases} \pi/3& \text{if } r \leq -1 \\ 0 & \text{if } r \geq 1\\ \frac{\cos^{-1}(r)}{3} &\text{otherwise} \end{cases} \]](form_1102.png)
And
![\[ r = \frac{(m_{xx} - q)(m_{yy} - q)(m_{zz} - q) + 2 m_{xy} m_{xz}m_{yz} - (m_{yy} - q) m_{xz}^2 - (m_{zz} - q) m_{xy}^2 - (m_{xx} - q) m_{yz}^2}{2 p^3} \]](form_1103.png)
Moreover, the 2d rotation angle 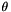 is replaced by the 3d rotation angles
is replaced by the 3d rotation angles 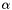 ,
, 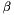 and
and 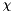 , calculated with the coefficients of
, calculated with the coefficients of 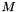 :
:
![\[ \begin{array}{r c l} \alpha & = & \tan^{-1} \left( \frac{m_{yz}}{m_{zz}} \right) \\ \beta & = & - \sin \left( m_{xz} \right) \\ \chi & = & \tan^{-1} \left( \frac{m_{xy}}{m_{xx}} \right) \end{array} \]](form_1105.png)
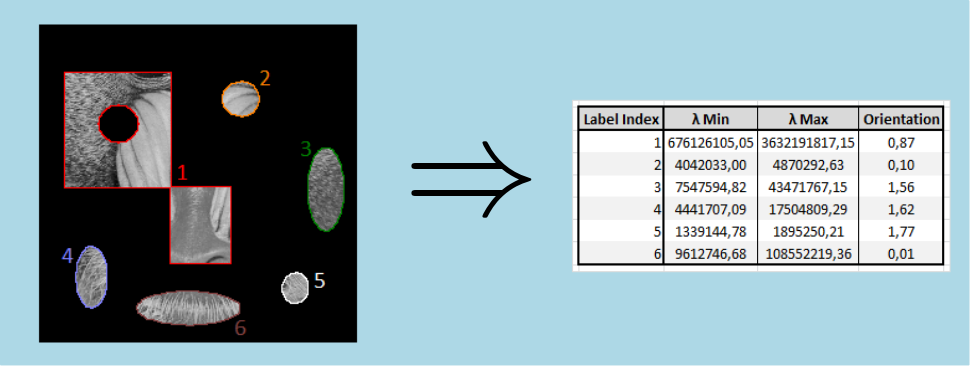
Here is an example of the grey inertia calculated from a 2d input image :
Measure allowing to compute the second order moment ponderated by the gray level of each pixel for shape
Measure synthesis :
| Measure Type | Measure Unit Type | Parameter Type | Result Type | Shape Requirements |

Intensity
|

None
|

None
|

Custom
|
Row Intersections
|
See Shape measurement for additional information on these pictograms Example of Python code :
Generic example in 2d case :
import PyIPSDK
import PyIPSDK.IPSDKIPLShapeAnalysis as shapeanalysis
inMeasureInfoSet2d = PyIPSDK.createMeasureInfoSet2d()
PyIPSDK.createMeasureInfo(inMeasureInfoSet2d, "GreyInertiaMsr")
outMeasureSet = shapeanalysis.labelAnalysis2d(inGreyImg, inLabelImg2d, inMeasureInfoSet2d)
PyIPSDK.saveCsvMeasureFile(os.path.join(tmpPath, "shape_analysis_results.csv"), outMeasureSet)
outMsr = outMeasureSet.getMeasure("GreyInertiaMsr")
outMsrValues = outMsr.getMeasureResult().getColl(0)
print("First label inertia mxx component measurement equal " + str(outMsrValues[1].mxx()))
Generic example in 3d case :
import PyIPSDK
import PyIPSDK.IPSDKIPLShapeAnalysis as shapeanalysis
inMeasureInfoSet3d = PyIPSDK.createMeasureInfoSet3d()
PyIPSDK.createMeasureInfo(inMeasureInfoSet3d, "GreyInertiaMsr")
outMeasureSet = shapeanalysis.labelAnalysis3d(inGreyImg, inLabelImg, inMeasureInfoSet3d)
PyIPSDK.saveCsvMeasureFile(os.path.join(tmpPath, "shape_analysis_results.csv"), outMeasureSet)
outMsr = outMeasureSet.getMeasure("GreyInertiaMsr")
outMsrValues = outMsr.getMeasureResult().getColl(0)
print("First label inertia mxx component measurement equal " + str(outMsrValues[1].mxx()))
Example of C++ code :
Example informations
Associated library
IPSDKIPLShapeAnalysis
Code Example
Shape2dCollPtr pShape2dColl = boost::make_shared<Shape2dColl>();
readFromXmlFile(inputShape2dCollPath, *pShape2dColl);
MeasureInfoSetPtr pMeasureInfoSet = MeasureInfoSet::create2dInstance();
createMeasureInfo(pMeasureInfoSet, "GreyInertiaMsr");
MeasureSetPtr pOutMeasureSet =
shapeAnalysis2d(pInGreyImg2d, pShape2dColl, pMeasureInfoSet);
const MeasureConstPtr& pGreyInertiaOutMsr = pOutMeasureSet->getMeasure("GreyInertiaMsr");
const GreyInertiaMsrResults& outResults = static_cast<const GreyInertiaMsrResults&>(pGreyInertiaOutMsr->getMeasureResult());

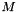 .
.![\[ M = \begin{bmatrix} m_{xx} & m_{xy} & m_{xz} \\ m_{yx} & m_{yy} & m_{yz} \\ m_{zx} & m_{zy} & m_{zz} \end{bmatrix} \]](form_1091.png)
![\[ \begin{array}{r c l} m_{xx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right)^2 I(x, y, z)} \\ m_{xy} = m_{yx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right) \left(y - \bar{y} \right) I(x, y, z)} \\ m_{xz} = m_{zx} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(x - \bar{x} \right) \left(z - \bar{z} \right) I(x, y, z)} \\ m_{yy} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(y - \bar{y} \right)^2 I(x, y, z)}\\ m_{yz} = m_{zy} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(y - \bar{y} \right) \left(z - \bar{z} \right) I(x, y, z)} \\ m_{zz} = m_{zz} & = & \sum_{\lbrace x, y, z \rbrace \in Shape}{ \left(z - \bar{z} \right) \left(z - \bar{z} \right) I(x, y, z)} \end{array} \]](form_1092.png)
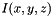 is the image intensity at the position
is the image intensity at the position 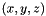 ,
, 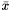 ,
, 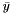 and
and 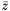 are the grey barycenter coordinates (see GreyBarycenter) and
are the grey barycenter coordinates (see GreyBarycenter) and 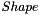 is the voxel collection of the current shape.
is the voxel collection of the current shape.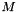 (
( 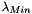 and
and 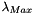 ) and the shape orientation
) and the shape orientation 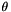 .
.![\[ \begin{array}{r c l} \delta & = & \sqrt{(m_{xx} - m_{yy}) (m_{xx} - m_{yy}) + 4 m_{xy} m_{xy}} \\ \lambda_{Max} & = & \frac{1}{2} \left( m_{xx} + m_{yy} + \delta \right) \\ \lambda_{Min} & = & \frac{1}{2} \left( m_{xx} + m_{yy} - \delta \right) \\ \theta & = & \tan^{-1} \left( \frac{\lambda_{Max} - m_{xx}}{m_{xy}} \right) \end{array} \]](form_1100.png)
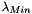 and
and 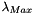 are proportional to the squared length of the eigenvector axes, represented by green arrows in the figure below.
are proportional to the squared length of the eigenvector axes, represented by green arrows in the figure below.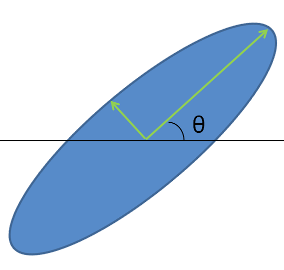
![\[ \begin{array}{r c l} q & = & \frac{m_{xx} + m_{yy} + m_{zz}}{3} \\ p & = & \sqrt{\frac{(m_{xx} - q)^2 + (m_{yy} - q)^2 + (m_{zz} - q)^2 + 2 (m_{xy}^2 + m_{xz}^2 + m_{yz}^2)}{6}} \\ \lambda_{Max} & = & q + 2 p \cos(\phi + 2 \pi / 3) \\ \lambda_{Inter} & = & q + 2 p \cos(\phi - 2 \pi / 3) \\ \lambda_{Min} & = & q + 2 p \cos(\phi) \end{array} \]](form_1101.png)
![\[ \phi = \begin{cases} \pi/3& \text{if } r \leq -1 \\ 0 & \text{if } r \geq 1\\ \frac{\cos^{-1}(r)}{3} &\text{otherwise} \end{cases} \]](form_1102.png)
![\[ r = \frac{(m_{xx} - q)(m_{yy} - q)(m_{zz} - q) + 2 m_{xy} m_{xz}m_{yz} - (m_{yy} - q) m_{xz}^2 - (m_{zz} - q) m_{xy}^2 - (m_{xx} - q) m_{yz}^2}{2 p^3} \]](form_1103.png)
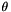 is replaced by the 3d rotation angles
is replaced by the 3d rotation angles 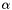 ,
, 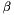 and
and 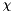 , calculated with the coefficients of
, calculated with the coefficients of 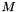 :
:![\[ \begin{array}{r c l} \alpha & = & \tan^{-1} \left( \frac{m_{yz}}{m_{zz}} \right) \\ \beta & = & - \sin \left( m_{xz} \right) \\ \chi & = & \tan^{-1} \left( \frac{m_{xy}}{m_{xx}} \right) \end{array} \]](form_1105.png)





 1.8.14
1.8.14