ClustersCenters =	kMeansPPClusterInit (inImg,inNbClusters)
ClustersCenters =	kMeansPPClusterInit (inImg,inOptSingleGreyMaskImg,inNbClusters)
ClustersCenters =	nonRandomKMeansPPClusterInit (inImg,inNbClusters)
ClustersCenters =	nonRandomKMeansPPClusterInit (inImg,inOptSingleGreyMaskImg,inNbClusters)

Detailed Description

Initializes the clusters for K-Mean classification.

Classical random K-means algorithm initialization can lead to a sub-optimal classification and can vary between two calculations. Defining a relevant cluster initialization is an important problem in order to produce a robust and repeatable classification.

This algorithm can compute two versions of the K-Means++ initialization algorithm :

The first implementation is based on a random approach [1].
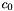1. The idea is to randomly generate the first center , just like for the classical K-Means.
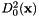2. A distance map $D^2_0(\textbf{x})$ is then compute between this center and each pixels of the image :
  $D^2_0(\textbf{x}) = \Vert InImg(\textbf{x}) - c_0 \Vert^2$
3. The new center is defined randomly, from the probability distribution
  $\frac{D^2_0(\textbf{x})}{\sum_{\textbf{x}}{D^2_0(\textbf{x})}}$
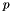  In other words, the cumulated distance map is calculated from the first pixel to the last element in the image. The probability is also generated in order to have $p \in \left[ 0, \sum_{\textbf{x}}{D^2_0(\textbf{x})} \right]$ . The new center is the first pixel where the cumulated distance is greater than .
4. The new distance map is calculated, keeping only the distance to the closest center :
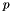  $D^2_i(\textbf{x}) = \min_{k \in \left[ 0, N \right]} (D^2_k(\textbf{x})), i > 0$
  Where N is the number of already defined centers.
5. The steps 3 and 4 are repeated until the algorithm found the requested number of centers.
The second implementation is a non random variant of the original K-Means ++ algorithm, which allows repeatable results :
1. The first center is the first pixel in the image.
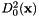2. The distance map $D^2_0(\textbf{x})$ is calculated as described above.
3. The new center is the pixel with the maximum distance.
4. Compute the new distance map, keeping the distance to the closest existing center.
5. Repeat the steps 3 and 4 until the algorithm finds the requested number of centers.

Here is an example of a non-random cluster center classification on a UInt8 gray-level image with 5 clusters:

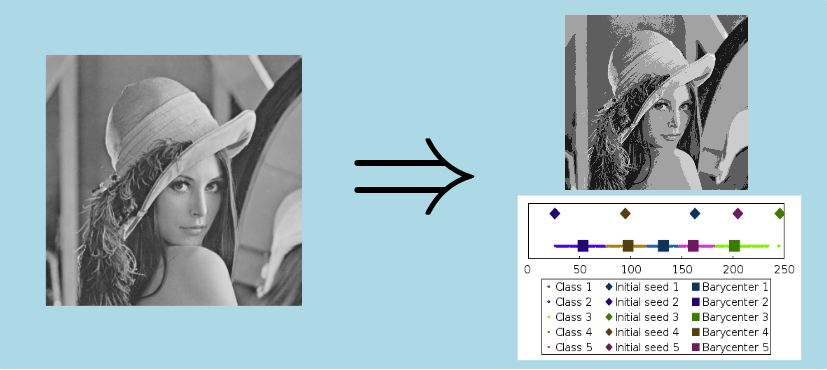
We can read on the abscissa axis the grey level intensity. The small points represent the pixels in the image, colored according to the cluster initialization. The squares illustrates the final cluster centers whereas the diamonds correspond to the first center as described in the step 1 of one of the algorithm versions.

If a mask image is provided, only pixels where the mask equals True can be used as a center. In the random case, the first center is randomly defined and until it corresponds to a value of False in the mask image. In the non-random case, the first center is the first pixel where the mask equals True: the first line is scanned, if all the pixels in the first line have False in the mask image, the second line is scanned, etc. To define the other centers, only pixels where the mask image equals True are used for the distance map calculation.

References

[1] "K-means++: The Advantages of Careful Seeding", Arthur, D. and Vassilvitskii, S, Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2007, 1027-1035

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLClassification as classif

Code Example

    # opening of input images
    geometry = PyIPSDK.geometryRgb2d(PyIPSDK.eImageBufferType.eIBT_Int8, sizeX, sizeY)
    inImg = PyIPSDK.loadRawImageFile(inputImgPath, geometry)
    
    # Random initialization
    outRandom = classif.kMeansPPClusterInit(inImg,  nbClusters)
    # Non-Random initialization
    outNonRandom = classif.nonRandomKMeansPPClusterInit(inImg,  nbClusters)
    
    # Access to the first randomly generated cluster center
    firstRandomClusterCenter = outRandom.coll[0].elements

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLClassification/Processor/KMeansPPClusterInit/KMeansPPClusterInit.h>

Code Example

    // Random approach
    // ---------------
    ClustersCentersPtr pClustersCenters_Random = kMeansPPClusterInit(pInImg, nbClusters);
    // Access to the first randomly generated cluster center elements
    ClusterCenterPtr randomClusterCenter = pClustersCenters_Random->getNodeColl<ClustersCenters::Coll>()[0];
    const std::vector<ipReal64>& vRandomClusterElements = randomClusterCenter->getLeafColl<ClusterCenter::Elements>();
    // Non-Random approach
    // ---------------
    ClustersCentersPtr pClustersCenters_NonRandom = nonRandomKMeansPPClusterInit(pInImg, nbClusters);