Measure allowing to compute Lowitz local histogram module.

This measure computes the local histogram module [1], of image pixel/voxel intensity values associated to a 2d/3d shape. The higher is the measure, the more homogeneous is the shape. Homogeneous shapes yields 1/NumericLimits<ipReal64>::epsilon().

This measure is based on the analysis of the shape histogram (see Histogram). Given the histogram parameters allowing to determine (among others) the number of classes 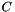$C$ and a global range for the histogram, this measure is computed as the Mahalanobis distance between the actual histogram 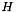$H$ and the theoretical histogram 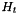$H_t$ for which each bin has the same value. This distance can be expressed as :

$d(H, H_t) = \sum_{i = 0}^{C-1}{\frac{\vert E(H_i) - E(H_{ti}) \vert}{\sqrt{\sigma^2(H_i) + \sigma^2(H_{ti})}}}$

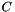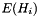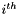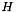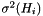Where $C$ is the number of classes in the histogram, $E(H_i)$ is the expected value of the $i^{th}$ bin of the histogram $H$ and $\sigma^2(H_i)$ is its variance.

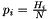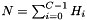Let us define $p_i$ as the value of the normalized histogram : $p_i = \frac{H_i}{N}$ , with $N = \sum_{i = 0}^{C-1}{H_i}$ being the number of pixels in the shape. Since this measure is based on Bernoulli distribution, the expected value of 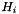$H_i$ and its variance are :

$E(H_i) = p_i$

$\sigma^2(H_i) = p_i \left( 1-p_i \right)$

Moreover the expected value (and hence probability) and variance of the theoretical histogram 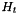$H_t$ for each bin 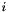$i$ are:

$E(H_{ti}) = \frac{1}{C}$

$\sigma^2(H_{ti}) = \frac{1}{C} \left( 1 - \frac{1}{C} \right)$

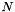With $N$ draws (1 per pixel in the shape), we can rewrite the Mahalanobis distance as follows :

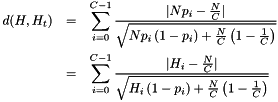
$\begin{eqnarray*} d(H, H_t) & = & \sum_{i = 0}^{C-1}{\frac{\vert N p_i - \frac{N}{C} \vert}{\sqrt{N p_i \left( 1 - p_i \right) + \frac{N}{C} \left( 1 - \frac{1}{C} \right)}}} \\ & = & \sum_{i = 0}^{C-1}{\frac{\vert H_i - \frac{N}{C} \vert}{\sqrt{H_i \left( 1 - p_i \right) + \frac{N}{C} \left( 1 - \frac{1}{C} \right)}}} \end{eqnarray*}$

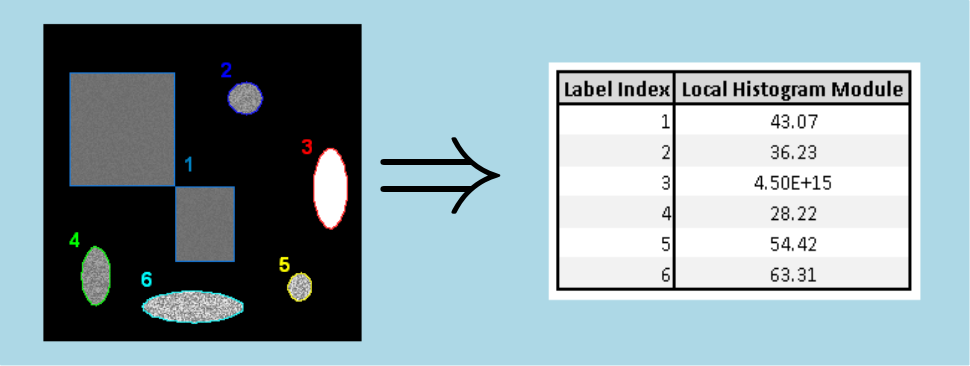
Here is an example of energy measurement in 2d case :

References

[1] G. Lowitz "Can a Local Histogram Really Map Texture Information?". Pattern Recognition, 16, 2, 1983, pp 141–147.

Measure allowing to compute Lowitz local histogram module

Measure synthesis :

Measure Type	Measure Unit Type	Parameter Type	Result Type	Shape Requirements
Generic	None	LocalHistogramModuleMsrParams	Value (ipsdk::ipReal64)	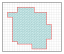Row Intersections

See Shape measurement for additional information on these pictograms

Example of Python code :

Generic example in 2d case :

import PyIPSDK

import PyIPSDK.IPSDKIPLShapeAnalysis as shapeanalysis

    # Create the infoset
    inMeasureInfoSet2d = PyIPSDK.createMeasureInfoSet2d()
    PyIPSDK.createMeasureInfo(inMeasureInfoSet2d, "LocalHistogramModuleMsr")
    
    #Perform the analysis
    outMeasureSet = shapeanalysis.labelAnalysis2d(inGreyImg, inLabelImg2d, inMeasureInfoSet2d)
    
    # save results to csv format
    PyIPSDK.saveCsvMeasureFile(os.path.join(tmpPath,  "shape_analysis_results.csv"), outMeasureSet)
    
    # retrieve measure results
    outMsr = outMeasureSet.getMeasure("LocalHistogramModuleMsr")
    
    # retrieve measure values
    outMsrValues = outMsr.getMeasureResult().getColl(0)
    print("First label measurement equal " + str(outMsrValues[1]))

Generic example in 3d case :

import PyIPSDK

import PyIPSDK.IPSDKIPLShapeAnalysis as shapeanalysis

    # Create the infoset
    inMeasureInfoSet3d = PyIPSDK.createMeasureInfoSet3d()
    PyIPSDK.createMeasureInfo(inMeasureInfoSet3d, "LocalHistogramModuleMsr")
    
    #Perform the analysis
    outMeasureSet = shapeanalysis.labelAnalysis3d(inGreyImg, inLabelImg, inMeasureInfoSet3d)
    
    # save results to csv format
    PyIPSDK.saveCsvMeasureFile(os.path.join(tmpPath,  "shape_analysis_results.csv"), outMeasureSet)
    
    # retrieve measure results
    outMsr = outMeasureSet.getMeasure("LocalHistogramModuleMsr")
    
    # retrieve measure values
    outMsrValues = outMsr.getMeasureResult().getColl(0)
    print("First label measurement equal " + str(outMsrValues[1]))

Example of C++ code :

Example informations

Associated library

IPSDKIPLShapeAnalysis

Code Example

    // opening grey level input image
    ImagePtr pInGreyImg2d = loadTiffImageFile(inputGreyImgPath);
    // read entity shape 2d collection used for processing
    Shape2dCollPtr pShape2dColl = boost::make_shared<Shape2dColl>();
    IPSDK_REQUIRE(readFromXmlFile(inputShape2dCollPath, *pShape2dColl) == true);
    // define a measure info set
    MeasureInfoSetPtr pMeasureInfoSet = MeasureInfoSet::create2dInstance();
    createMeasureInfo(pMeasureInfoSet, "LocalHistogramModuleMsr");
    
    // compute measure on shape 2d collection
    MeasureSetPtr pOutMeasureSet = shapeAnalysis2d(pInGreyImg2d, pShape2dColl, pMeasureInfoSet);
    // retrieve associated results
    const MeasureConstPtr& pLocalHistogramModuleOutMsr = pOutMeasureSet->getMeasure("LocalHistogramModuleMsr");
    const ipsdk::shape::analysis::ValueMeasureResult<ipsdk::ipReal64>& outResults = static_cast<const ipsdk::shape::analysis::ValueMeasureResult<ipsdk::ipReal64>&>(pLocalHistogramModuleOutMsr->getMeasureResult());