 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
| image = | multiscaleVesselEnhancement3dImg (inImg3d,inMVEParams) |
Multiscale vessel enhancement using Frangi's approach on 3d images.
The MultiscaleVesselEnhancement3dImg algorithm is the extension of the Multiscale vessel enhancement 2d algotihm to the 3d case. It is an iterative approach used to enhance tube-like features in an image where each scale focuses on a specific tube width range.
The algorithm steps are applied for each voxel, for this reason, we avoid the notation of the coordinates 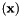 in the following. For a given scale
in the following. For a given scale 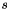 , the algorithm computes at each voxel the Hessian matrix
, the algorithm computes at each voxel the Hessian matrix 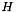 . Its eigen values
. Its eigen values 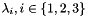 are then extracted and sorted in order to identify :
are then extracted and sorted in order to identify :
![\[ \vert \lambda_1 \vert \leq \vert \lambda_2 \vert \leq \vert \lambda_3 \vert \]](form_628.png)
For an ideal tubular structure, we have:
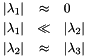
A blobness coefficient 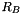 and a structureness coefficient
and a structureness coefficient 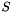 are then calculated from
are then calculated from 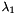 ,
, 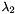 and
and 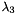 :
:
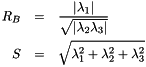
A third coefficient 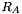 , referring to the aspect ratio of the two largest second order derivatives, is also calculated:
, referring to the aspect ratio of the two largest second order derivatives, is also calculated:
![\[ R_A = \frac{\vert \lambda_2 \vert}{\vert \lambda_3 \vert} \]](form_632.png)
This value allows to distinguish plate-like structures from line-like structures ( 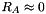 in the latter case).
in the latter case).
The vesselness for a scale 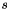 , noted
, noted 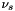 , is finally computed as a combination of these coefficients. For bright features on dark background, this measure can be expressed as:
, is finally computed as a combination of these coefficients. For bright features on dark background, this measure can be expressed as:
![\[ \nu_s = \begin{cases} 0 & \text{if } \lambda_2 > 0 \text{ or } \lambda_3 > 0\\ \left( 1 - \exp \left(-\frac{R_A^2}{2 \alpha^2} \right) \right) \exp \left(-\frac{R_B^2}{2 \beta^2} \right) \left( 1 - \exp \left(-\frac{S^2}{2c^2} \right) \right) & \text{otherwise} \end{cases} \]](form_634.png)
Where 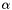 ,
, 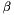 and
and 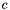 are sensitivity thresholds for each coefficients.
are sensitivity thresholds for each coefficients. 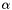 and
and 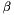 are input parameters and
are input parameters and 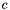 is calculated as:
is calculated as:
![\[ c = \frac{1}{2} \max_{\textbf{x} \in \Omega} \left( \Vert H(\textbf{x}) \Vert \right) \]](form_616.png)
Where 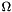 is the image domain and
is the image domain and 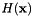 is the Hessian matrix of the image at voxel
is the Hessian matrix of the image at voxel 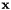 .
.
For dark features on bright background, the condition 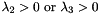 becomes
becomes 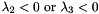 .
.
The final result is an image containing the maximum value of 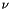 along all the scales on each pixel:
along all the scales on each pixel:
![\[ \nu(\textbf{x}) = \max_{s \in Scales}\left( \nu_s(\textbf{x}) \right) \]](form_622.png)
Where 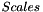 is the collection of scales given as input parameter.
is the collection of scales given as input parameter.
The algorithm parametrization is done using the MVEParams data item, which contains:
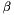 threshold (by default,
threshold (by default, 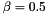 ),
),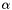 threshold (by default,
threshold (by default, 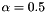 ).
).Moreover, the algorithm allows the user to provide a class image, with type UInt8. If this image is set, the algorithm will fill it by the scale index corresponding to the maximum 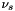 :
:
![\[ OutOptClassImg(\textbf{x}) = argmax_{s \in Scales}\left( \nu_s(\textbf{x}) \right) \]](form_625.png)
See Multiscale vessel enhancement 2d for a 2d illustration of multiscale vessel enhancement.