image = qrSolverImg (inSeqImg1,inSeqImg2,inNbFeatures)

Detailed Description

Solves an overdeterminated system Ax=b for each pixel using a QR decomposition.

In some cases, it can be necessary to find the parameters of an analytic model. States before and after applying the model are known, but the way the data are transformed is a black box. A common example is finding the motion field between two images. In that example, positions in both images are known but we want to model the displacement for all pixels

Such a transform can be expressed as an overdetermined linear system 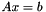$Ax=b$ . Where 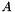$A$ is a set of data, covering several features (for example gratients) on several images, 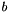$b$ is a known result we want to reach with an estimate of the linear model parametrized by the coefficients of $x$ .

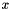We have here more equations than unknowns. The most ordinary way to solve the solution is the least squares method :

$x = (A^T A)^{-1} A^T b$

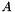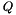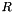To efficiently achieve this calculation, it is possible to decompose $A$ into two matrices $Q$ and $R$ . We can rewrite the problem :

$Ax=b \Leftrightarrow QRx=b \Leftrightarrow Rx=Q^{-1} b$

The first advantage of this factorization is that 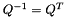$Q^{-1} = Q^T$ , we can rewrite the previous equation :

$Rx=Q^T b$

The second advantage is that 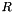$R$ is diagonal, we can easily solve the system. We choose the Householder reflection to achieve the decomposition.

Given two images InSeqImg1 and InSeqImg2, this algorithm solves the system to find the parameters x, stored in the image OutRealSeqImg.

The input image InSeqImg1 is assigned to 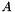$A$ , whereas the vector 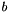$b$ is represented by InSeqImg2. For each pixel, the coefficients are stored along the temporal dimensions. In the case of InSeqImg1, we use a row-major representation of the matrix $A$ .

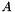The temporal size of 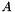$A$ equals the temporal size of 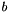$b$ multiplied by the temporal size of 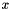$x$ , and the temporal size of 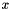$x$ equals the number of features used in the linear system.

See also: https://en.wikipedia.org/wiki/Overdetermined_system; https://en.wikipedia.org/wiki/QR_decomposition

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLLinearAlgebra as la

Code Example

imX = la.qrSolverImg(imA, imB, nbFeatures)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLLinearAlgebra/Processor/QRSolverImg/QRSolverImg.h>

Code Example

            // We want to solve the system Ax=b for each pixel,
            // where the coefficients are stored along the temporal dimensions
            // Sample with a generated output image
            // ------------------------------------
            // Solve the QR system
            ImagePtr pAutoOutImg = qrSolverImg(pInImgA, pInImgB, nbFeatures);
            // Sample with a provided output image
            // -----------------------------------
            // create output image
            ImageGeometryPtr pOutputImageGeometry = geometrySeq2d(eImageBufferType::eIBT_Real32, sizeX, sizeY, nbFeatures);
            boost::shared_ptr<MemoryImage> pOutImg(boost::make_shared<MemoryImage>());
            pOutImg->init(*pOutputImageGeometry);
            // compute square value of input image
            qrSolverImg(pInImgA, pInImgB, nbFeatures, pOutImg);