Features2dRegistrationResult =	greySignedFeatures2dRegistration (inGreySignatures2d1,inGreySignatures2d2)
Features2dRegistrationResult =	greySignedFeatures2dRegistration (inGreySignatures2d1,inGreySignatures2d2,inRegMotionModel2d,inCorrelationThreshold2d,inOptRegistrationEstimationConfig)

Detailed Description

algorithm allowing registration of features 2d associated to grey signature

This algorithm allows automatic computation of a motion transform linking two sets of grey signed features 2d.

This algorithm is composed of two main phasis.

a pairing phasis :

During this phasis, features from first input collection 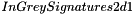$InGreySignatures2d1$ are associated to features from second collection 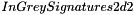$InGreySignatures2d2$ . We consider this assignment problem of two sets of input grey signed features 2d as a weighted bipartite assignment problem using correlation of feature signatures as distance. Parameter 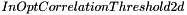$InOptCorrelationThreshold2d$ allows to exclude pairs with low correlation value.

a robust motion transform computation phasis :

Robust motion transform computation is by default based on a least median of squares regression technique. This allows to detect and remove outliers formed during pairing phasis. Note that this specific algorithm make the assuption of an outlier ratio lower than 50% (use RANSAC like algorithm to avoid this limitation). Parameter 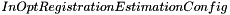$InOptRegistrationEstimationConfig$ allows to customize behavior of this phasis. See Parametric estimation for more informations on this stage.

Type of computed transformation is controled by 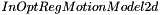$InOptRegMotionModel2d$ parameter.

On output algorithm returned a registration result composed of :

used origin feature signatures
used target feature signatures
the computed transformation allowing to transform data of origin image to target image :
$P_{target}=sR(\theta)P_{origin} + T(T_x, T_y)$
with :
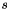- a scale factor computed in similarity case (ie. ipsdk::imaproc::attr::eRegistrationMotionModel2d::eRMM2d_Similarity) and equal to 1 in rigid case (ie. ipsdk::imaproc::attr::eRegistrationMotionModel2d::eRMM2d_Rigid).
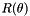- $R(\theta)$ a rotation matrix, see Rotations 2d.
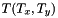- a translation vector
the computed transformation can also be of form :
$\bar{P}_{target}=H \bar{P}_{origin}$
in case of homography motion model (ipsdk::imaproc::attr::eRegistrationMotionModel2d::eRMM2d_Homography) with :
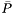- $\bar{P}$ homogeneous coordinates associated to point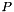
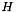- a 3x3 matrix
a structure agregating indicators about registration results :
- the number of input features in first and second collections
- the number of pairs formed from these two collections (result of pairing phasis)
- the status of robust estimation (see following remark)
- number of detected outliers (greater than 0 if robust estimation has been successfully proceeded)
- root mean square of residuals (rms) :
  $\sqrt{\sum_{i=0}^{nbPairs}{\left \|P^i_{target}-\left(sR(\theta)P^i_{origin} + T(T_x, T_y)\right)\right \|^2}}$
- the collection of made assignments with their coordinates, the associated weight and a flag used to store outlier status of assignment.

Structure agregating indicators should be carefully analyzed by user to check reliability of computed results. Here are some clues to avoid classical pits in robust estimation :

check status of robust estimation, in case where flag RobustEstimationDone is set to false in RobustEstimationResults result structure, algorithm do not have enough pairs of features to process to a robust estimation and switch to simple (non robust) estimation. In this case, algorithm will not support presence of outliers into input data set.
check number of detected outliers, remember that used robust algorithm make the assumption of an outlier ratio lower than 50% (by default).
check value of output rms : a great value for rms means that features are not correctly matched.

Here is an example of usage of this algorithm in case of rigid transform computation :

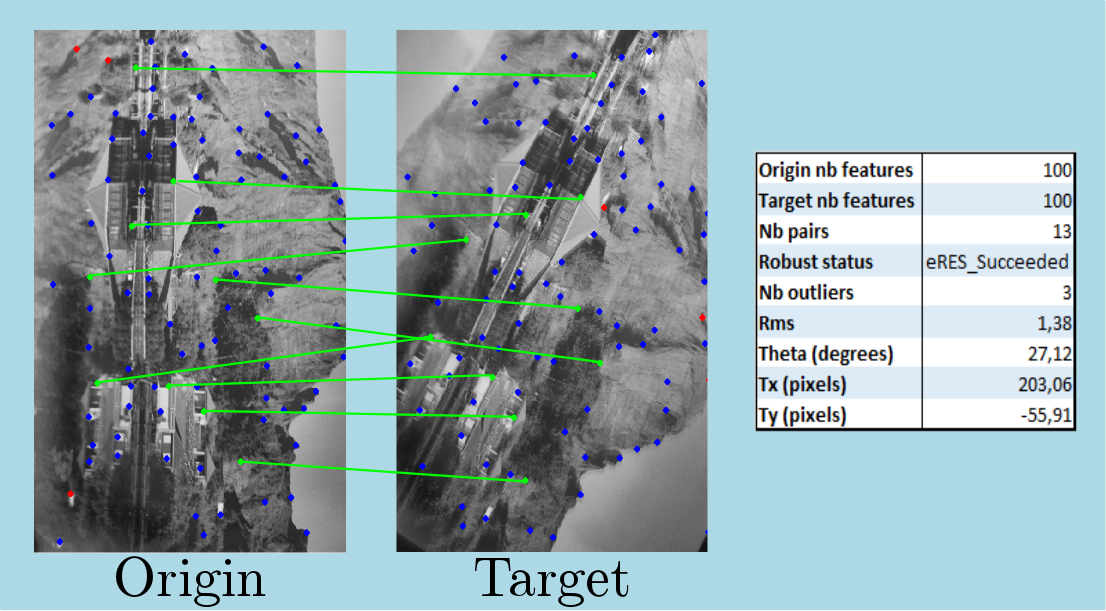
In this case, user can see that we provide two input collections of grey signed features with 100 elements for each. Given used correlation threshold (set to 0.95 in this case), only 13 made pairs are keeped (blue points stands for rejected data during pairing phasis).

This allows a robust computation of rigid transformation which detects 3 outliers in input collections (red points) leaving 10 inliers (green points linked between images).

On output algorithm estimates a root mean square of residuals equal to 1.38 pixels which grants a good estimation of transformation.

See also: https://en.wikipedia.org/wiki/Robust_regression

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLRegistration as registration

Code Example

    # opening of input images
    inImg1 = PyIPSDK.loadTiffImageFile(inputImgPath1)
    inImg2 = PyIPSDK.loadTiffImageFile(inputImgPath2)
    
    # extraction of grey signed features from first image
    greySignatures1 = registration.extractGreySignedFeatures2d(inImg1, 100)
    
    # extraction of grey signed features from second image
    greySignatures2 = registration.extractGreySignedFeatures2d(inImg2, 100)
    
    # computation of motion transform between images
    correlationThreshold = 0.95
    estimationConfig = PyIPSDK.EstimationConfig()
    estimationConfig.initLMS(0.48)
    outRegistrationResult = registration.greySignedFeatures2dRegistration(greySignatures1,
                                                                          greySignatures2,
                                                                          PyIPSDK.eRegistrationMotionModel2d.eRMM2d_Similarity,
                                                                          correlationThreshold, estimationConfig)
    transformParams = outRegistrationResult.transform.params
    
    # print of results
    print("Registration results :")
    print("----------------------")
    print("Nb original features : " + str(outRegistrationResult.indicators.nbFeatures1))
    print("Nb target features : " + str(outRegistrationResult.indicators.nbFeatures2))
    print("Nb made pairs : " + str(outRegistrationResult.indicators.nbPairs))
    print("Robust estimation status :")
    print("--------------------------")
    print(outRegistrationResult.indicators.estimationResults.toString())
    print("Estimated motion transform :")
    print("----------------------------")
    print("Scale factor : " + str(transformParams[PyIPSDK.Similarity2d.eTP_Scale]))
    print("Rotation (theta in radians) : " + str(transformParams[PyIPSDK.Similarity2d.eTP_Theta]))
    print("Translation : {" + str(transformParams[PyIPSDK.Similarity2d.eTP_Tx]) + ", " + str(transformParams[PyIPSDK.Similarity2d.eTP_Ty]) + "}")

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLRegistration/Processor/GreySignedFeatures2dRegistration/GreySignedFeatures2dRegistration.h>

#include <IPSDKIPL/IPSDKIPLRegistration/Processor/ExtractGreySignedFeatures2d/ExtractGreySignedFeatures2d.h>

Code Example

    // Load the input images
    ImagePtr pInImg1 = loadTiffImageFile(inImgFilePath1);
    ImagePtr pInImg2 = loadTiffImageFile(inImgFilePath2);
    // extraction of grey signed features from first image
    Features2dGreySignaturePtr pGreySignatures1 = extractGreySignedFeatures2d(pInImg1, 100);
    // extraction of grey signed features from seconde image
    Features2dGreySignaturePtr pGreySignatures2 = extractGreySignedFeatures2d(pInImg2, 100);
    // computation of motion transform between images
    const ipReal64 correlationThreshold = 0.95;
    const ipReal64 expectedOutlierRatio = 0.48;
    Features2dRegistrationResultPtr pOutRegistrationResult = greySignedFeatures2dRegistration(pGreySignatures1, pGreySignatures2,
                                                                                              eRegistrationMotionModel2d::eRMM2d_Similarity,
                                                                                              correlationThreshold,
                                                                                              createLMSRobustEstimationConfig(expectedOutlierRatio));
    const RegistrationMotionTransform2d& outTransform = pOutRegistrationResult->getNode<Features2dRegistrationResult::Transform>();