 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
| distImg,distWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg) |
| distImg,distWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg,pixelXSize,pixelYSize,neighborhood2d) |
| DistWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg,pixelXSize,pixelYSize,neighborhood2d,outDistImg) |
| distImg,distWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg,maxDistance) |
| distImg,distWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg,pixelXSize,pixelYSize,neighborhood2d,maxDistance) |
| DistWeight2d = | seededDistanceMap2dImg (inBinImg,inBinSeedImg,pixelXSize,pixelYSize,neighborhood2d,maxDistance,outDistImg) |
seeded distance map transform of an input binary image according to a seeded image
2d seeded distance map algorithm allows to compute the distance to the closest seeded pixel in a region for each pixel of this region, according to the given pixel size. As in Generic Seeded Distance Map 2d, the region is defined by a binary image with pixel intensities set to 1. The seeded pixels are defined by a seeded image with pixel intensities set to 1. If the parameter 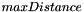 is provided, the propagation is constrained so that it stops when the distance is higher than the
is provided, the propagation is constrained so that it stops when the distance is higher than the 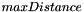 value.
value.
The resulting image buffer type must be one of the following :
Output image values are given by :
![\[ OutDistImg[x, y] = \left\{ \begin{array}{rl} 0 &\mbox{\text{if } InBinImg[x, y] = 0} \\ 1 &\mbox{\text{if } InBinImg[x, y] \text{is a seeded pixel}} \\ \min\limits_{(x_d, y_d) \in \aleph \wedge InBinImg[x_d, y_d] > 0}{\left( InBinImg[x_d, y_d]+\omega_d \right)} &\mbox{otherwise} \end{array} \right. \]](form_25.png)
Where 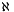 is the pixel's neighbourhood,
is the pixel's neighbourhood, 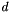 is the set of directions allowed by
is the set of directions allowed by 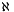 and can be lateral (along the x-axis), axial (along the y-axis) or diagonal.
and can be lateral (along the x-axis), axial (along the y-axis) or diagonal. 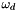 is the weight corresponding to the direction
is the weight corresponding to the direction 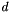 .
.
For a real output distance image, the weighting coefficients are set to 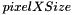 and
and 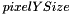 along the x (
along the x ( 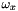 ) and y (
) and y ( 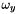 ) directions respectively and the diagonal weighting coefficient is set to
) directions respectively and the diagonal weighting coefficient is set to 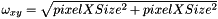 .
.
However, in the case of integer output, the coefficients are calculated in order to achieve the calculation with a good compromise between accuracy and computation efficiency [1]. In this case, the weights 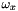 ,
, 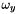 and
and 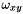 are calculated as described in the following algorithm :
are calculated as described in the following algorithm :
1- For simplicity in the notation, let 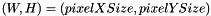 be the size of a pixel.
be the size of a pixel.
2- Compute the real coefficient along the y axis:
![\[ d_y = \frac{-2 H + 2 H \sqrt{1+\lambda}}{\lambda} \]](form_33.png)
with
![\[ \lambda = \frac{ \sqrt{W^2 + H^2 } - H}{W^2} \]](form_34.png)
3- Compute the other coefficients :
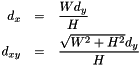
4- Compute the integer approximation 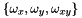 of the coefficients
of the coefficients 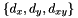 .
.
a- For this, we assume that que maximum calculable distance is 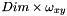 , where
, where 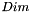 is the maximum between the output image width and the output image height.
is the maximum between the output image width and the output image height.
b- An integer scale factor 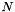 can then be computed. It must be large enough to allow a good approximation to the Euclidian distance and small enough to avoid overflow due to the output image type limitation.
can then be computed. It must be large enough to allow a good approximation to the Euclidian distance and small enough to avoid overflow due to the output image type limitation.
![\[ N \leq \frac{2^b}{Dim \times d_{xy}} \]](form_41.png)
Where 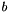 is the number of bits used to encode the each element of the distance map (e.g.
is the number of bits used to encode the each element of the distance map (e.g. 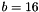 for an unsigned short distance map).
for an unsigned short distance map).
c- The integer distance weighting coefficients can now be calculated as follows :

5- Finally, the original scale must be retrieved and the resulting image is divided by 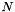 .
.
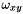 is set to 0 and the neighbourhood along the xy-direction are not used in the distance calculation.
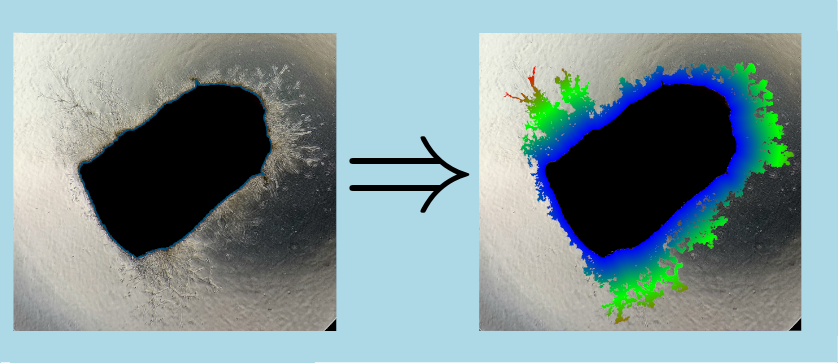
is set to 0 and the neighbourhood along the xy-direction are not used in the distance calculation.Here is an example of a 2d seeded distance map computation applied to a binary input image with a real result image. The seeds are displayed in red in the bottom sub-images and the neighborhood was set to 8-connexity :
[1] "Contribution a la comparaison d'images pour l'evaluation des traitements, la reconnaissance de formes et l'indexation des sequences d'images", Didier COQUIN, HDR, 2007