distImg,distWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d)
distImg,distWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d,pixelXSize,pixelYSize,pixelZSize,neighborhood3d)
DistWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d,pixelXSize,pixelYSize,pixelZSize,neighborhood3d,outDistImg)
distImg,distWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d,maxDistance)
distImg,distWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d,pixelXSize,pixelYSize,pixelZSize,neighborhood3d,maxDistance)
DistWeight3d =	seededDistanceMap3dImg (inBinImg3d,inBinSeedImg3d,pixelXSize,pixelYSize,pixelZSize,neighborhood3d,maxDistance,outDistImg)

Detailed Description

seeded distance map transform of a 3d input binary image according to a 3d seeded image

3d seeded distance map algorithm is the 3d extension of Seeded Distance Map 2d. It allows to compute the distance to the closest seeded voxel in a region for each voxel of this region, according to the given voxel size. The region is defined by a binary volume with voxel intensities set to 1. The seeded voxels are defined by a seeded volume with voxel intensities set to 1. If the parameter 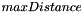$ maxDistance $ is provided, the propagation is constrained so that it stops when the distance is higher than the 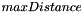value.

The resulting image buffer type must be one of the following :

ipsdk::image::eImageBufferType::eIBT_UInt16
ipsdk::image::eImageBufferType::eIBT_UInt32
ipsdk::image::eImageBufferType::eIBT_Real32

Just like Seeded Distance Map 2d, the voxel size parameters are used to compute the distance weighting coefficients to calculate the resulting distance map. In the case of integer output distance map, these coefficients are calculated as described in the folowwing algorithm [1] :

1- For simplicity in the notation, let 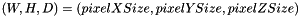$(W, H, D) = (pixelXSize, pixelYSize, pixelZSize)$ be the size of a voxel.

2- Compute the real coefficient along the x-axis:

$d_x = \frac{-2 + 2 \sqrt{1 + \lambda}}{\lambda}$

with

$\lambda = \left(\sqrt{2}-1\right)^2 + \frac{1}{D^2} \left(\sqrt{2+P^2}-\sqrt{2}\right)^2$

3- Compute the other coefficients :

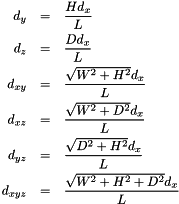
$\begin{eqnarray*} d_y & = & \frac{ H d_x }{L} \\ d_z & = & \frac{ D d_x }{L} \\ d_{xy} & = & \frac{ \sqrt{W^2 + H^2 } d_x }{L} \\ d_{xz} & = & \frac{ \sqrt{W^2 + D^2 } d_x }{L} \\ d_{yz} & = & \frac{ \sqrt{D^2 + H^2 } d_x }{L} \\ d_{xyz} & = & \frac{ \sqrt{W^2 + H^2 + D^2 } d_x }{L} \end{eqnarray*}$

4- Compute the integer approximation of the real coefficients.

a- For this, we assume that the maximum calculable distance is 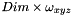$Dim \times \omega_{xyz}$ , where 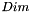$Dim$ is the maximum between the output volume width, the output volume height and the output volume depth.

b- An integer scale factor 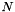$N$ can then be computed. It must be large enough to allow a good approximation to the Euclidian distance and small enough to avoid overflow due to the output image type limitation.

$N \leq \frac{2^b}{Dim \times d_{xyz}}$

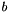Where $b$ is the number of bits used to encode the each element of the distance map (e.g. 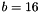$b = 16$ for an unsigned short distance map).

c- The integer distance weighting coefficients can now be calculated as follows :

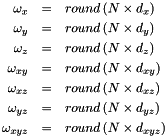
$\begin{eqnarray*} \omega_x & = & round \left( N \times d_x \right) \\ \omega_y & = & round \left( N \times d_y \right) \\ \omega_z & = & round \left( N \times d_z \right) \\ \omega_{xy} & = & round \left( N \times d_{xy} \right) \\ \omega_{xz} & = & round \left( N \times d_{xz} \right) \\ \omega_{yz} & = & round \left( N \times d_{yz} \right) \\ \omega_{xyz} & = & round \left( N \times d_{xyz} \right) \end{eqnarray*}$

5- Finally, the original scale must be retrieved and the resulting image is divided by 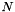$N$ .

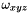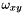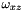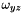Note: If the user defines a 18-connexity with the ipsdk::eNeighborhood3dType parameter, $\omega_{xyz}$ is set to 0 and the neighbourhood along the xyz-direction is not used in the distance calculation. Moreover, if the user defines a 6-connexity, $\omega_{xy}$ , $\omega_{xz}$ and $\omega_{yz}$ are also set to 0.

Here is an example of a 3d seeded distance map computation applied to a binary input image with a real result image with an 26-connexity neighbourhood :

References

[1] "Contribution a la comparaison d'images pour l'evaluation des traitements, la reconnaissance de formes et l'indexation des sequences d'images", Didier COQUIN, HDR, 2007

See also: Seeded Distance Map 2d

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLAdvancedMorphology as advmorpho

Code Example

    # opening of input images
    inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
    inSeedsImg = PyIPSDK.loadTiffImageFile(inputSeedsImgPath)
    
    # seeded distance map 3d computation
    outDistImg, outDistWeight3d = advmorpho.seededDistanceMap3dImg(inImg, inSeedsImg)
    xWeight = outDistWeight3d.xWeight
    yWeight = outDistWeight3d.yWeight
    zWeight = outDistWeight3d.zWeight
    xyWeight = outDistWeight3d.xYWeight
    xzWeight = outDistWeight3d.xZWeight
    yzWeight = outDistWeight3d.yZWeight
    xyzWeight = outDistWeight3d.xYZWeight

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLAdvancedMorphology/Processor/SeededDistanceMap3dImg/SeededDistanceMap3dImg.h>

Code Example

    // opening input image
    ImagePtr pInBinImg = loadTiffImageFile(inputImgPath, eTiffDirectoryMode::eTDM_Volume, eTiffBufferMode::eTBM_Binary);
    // opening seed input image
    ImagePtr pInSeedImg = loadTiffImageFile(inputSeedImgPath);
        
    // Define the size of the pixels
    const ipReal64 pixelXSize = 1.;
    const ipReal64 pixelYSize = 1.;
    const ipReal64 pixelZSize = 1.;
    // define output image geometry
    ImageGeometryPtr pDistGeometry = geometry3d(outputImageBufferType,
                                                pInBinImg->getSizeX(),
                                                pInBinImg->getSizeY(),
                                                pInBinImg->getSizeZ());
    // creation of output image
    boost::shared_ptr<MemoryImage> pOutDistImg(boost::make_shared<MemoryImage>());
    pOutDistImg->init(*pDistGeometry);
        
    // compute distance map on input image
    DistWeight3dPtr pDistWeight3d = seededDistanceMap3dImg(pInBinImg, pInSeedImg, pixelXSize, pixelYSize, pixelZSize, neighborhood3dType, pOutDistImg);
    // retrieve computed weights
    const ipReal64 XWeight = pDistWeight3d->getValue<DistWeight3d::XWeight>();
    const ipReal64 YWeight = pDistWeight3d->getValue<DistWeight3d::YWeight>();
    const ipReal64 ZWeight = pDistWeight3d->getValue<DistWeight3d::ZWeight>();
    const ipReal64 XYWeight = pDistWeight3d->getValue<DistWeight3d::XYWeight>();
    const ipReal64 XZWeight = pDistWeight3d->getValue<DistWeight3d::XZWeight>();
    const ipReal64 YZWeight = pDistWeight3d->getValue<DistWeight3d::YZWeight>();
    const ipReal64 XYZWeight = pDistWeight3d->getValue<DistWeight3d::XYZWeight>();