image =	separatedBilateral2dImg (inImg,inSpaceSigma,inRangeSigma)
image =	separatedBilateral2dImg (inImg,inHalfKnlSize,inSpaceSigma,inRangeSigma)

Detailed Description

separated version of bilateral filter on 2d image

The separated bilateral filter is an approximation of the Bilateral smoothing 2d that gives resulting images that may be close to what is obtained with the original bilateral filter with dramatically better time performance. The separated bilateral filter is executed in 2 passes: first along x-axis, then along y-axis.

Output image pixel values are given by:

$OutImg[x, y] = \dfrac { \sum_{o_y=-n}^{n}{W_y(x, y, o_y)*OutImg_x[x, y+o_y]} } { \sum_{o_y=-n}^{n}{W_y(x, y, o_y)} }$

where:

$OutImg_x[x, y] = \dfrac { \sum_{o_x=-n}^{n}{W_x(x, y, o_x)*InImg[x+o_x, y]} } { \sum_{o_x=-n}^{n}{W_x(x, y, o_x)} }$
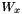is the weight function along x-axis;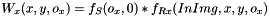 $W_x(x, y, o_x)=f_S(o_x, 0)*f_{Rx}(InImg, x, y, o_x)$
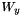is the weight function along y-axis;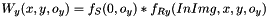 $W_y(x, y, o_y)=f_S(0, o_y)*f_{Ry}(InImg, x, y, o_y)$
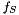is the space function;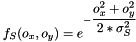 $f_S(o_x, o_y)=e^{-\dfrac{o_x^2+o_y^2}{2*\sigma_S^2}}$
$f_{Rx}(InImg, x, y, o_x)= \begin{cases} 1, & \text{if } o_x=0 \\ f_R(|InImg[x, y]-InImg[x+o_x, y]|), & \text{if } o_x > 0 \text { and } f_R(|InImg[x, y]-InImg[x+o_x, y]|) < f_{Rx}(x, y, o_x-1) \\ f_{Rx}(x, y, o_x-1), & \text{if } o_x > 0 \text { and } f_R(|InImg[x, y]-InImg[x+o_x, y]|) \geq f_{Rx}(x, y, o_x-1) \\ f_R(|InImg[x, y]-InImg[x+o_x, y]|), & \text{if } o_x < 0 \text { and } f_R(|InImg[x, y]-InImg[x+o_x, y]|) < f_{Rx}(x, y, o_x+1) \\ f_{Rx}(x, y, o_x+1), & \text{if } o_x < 0 \text { and } f_R(|InImg[x, y]-InImg[x+o_x, y]|) \geq f_{Rx}(x, y, o_x+1) \end{cases}$
$f_{Ry}(InImg, x, y, o_y)= \begin{cases} 1, & \text{if } o_y=0 \\ f_R(|InImg[x, y]-InImg[x, y+o_y]|), & \text{if } o_y > 0 \text { and } f_R(|InImg[x, y]-InImg[x, y+o_y]|) < f_{Ry}(x, y, o_y-1) \\ f_{Ry}(x, y, o_y-1), & \text{if } o_y > 0 \text { and } f_R(|InImg[x, y]-InImg[x, y+o_y]|) \geq f_{Ry}(x, y, o_y-1) \\ f_R(|InImg[x, y]-InImg[x, y+o_y]|), & \text{if } o_y < 0 \text { and } f_R(|InImg[x, y]-InImg[x, y+o_y]|) < f_{Ry}(x, y, o_y+1) \\ f_{Ry}(x, y, o_y+1), & \text{if } o_y < 0 \text { and } f_R(|InImg[x, y]-InImg[x, y+o_y]|) \geq f_{Ry}(x, y, o_y+1) \end{cases}$
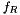is the range function;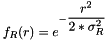 $f_R(r)=e^{-\dfrac{r^2}{2*\sigma_R^2}}$
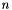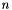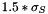is defined by InOptHalfKnlSize attribute (if this attribute is not initialized, then equals to $1.5*\sigma_S$ )
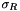$\sigma_R$ is defined by InRangeSigma attribute
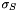$\sigma_S$ is defined by InSpaceSigma attribute

Input and output images must have same size.

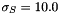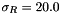Here is an example of a separated bilateral 2d operation applied to an 8-bits grey levels input image (with $\sigma_S=10.0$ and $\sigma_R=20.0$ ):

See also: M. Moreaud, F. Cokelaer, Flowing Bilateral Filter : definition and GPU implementation, Image Analysis and Stereology (revision in progress)

Example of Python code :

Example imports

import PyIPSDK

import PyIPSDK.IPSDKIPLFiltering as filter

Code Example

    # opening of input images
    inImg = PyIPSDK.loadTiffImageFile(inputImgPath)
    
    # separable bilateral filter 2d computation
    outImg = filter.separatedBilateral2dImg(inImg, 5, 3)

Example of C++ code :

Example informations

Header file

#include <IPSDKIPL/IPSDKIPLFiltering/Processor/SeparatedBilateral2dImg/SeparatedBilateral2dImg.h>

Code Example

        // definition of a custom output geometry
        ImageGeometryPtr pOutImageGeometry =
            geometry2d(outImageBufferType,
                       pInImg->getSizeX(),
                       pInImg->getSizeY());
        // creation of output image
        boost::shared_ptr<MemoryImage> pOutImg = boost::make_shared<MemoryImage>();
        pOutImg->init(*pOutImageGeometry);
        // compute bilateral filter on input image
        separatedBilateral2dImg(pInImg, inHalfKnlSize, inSpaceSigma, inRangeSigma, pOutImg);