 |
IPSDK 4.1.1.1
IPSDK : Image Processing Software Development Kit
|
| xGradImg,yGradImg,zGradImg = | sobelGradient3dImg (inImg) |
| xGradImg,yGradImg,zGradImg = | sobelGradient3dImg (inImg,kernelType,bNormalize) |
| image = | sobelXGradient3dImg (inImg) |
| image = | sobelXGradient3dImg (inImg,kernelType,bNormalize) |
| image = | sobelYGradient3dImg (inImg) |
| image = | sobelYGradient3dImg (inImg,kernelType,bNormalize) |
| image = | sobelZGradient3dImg (inImg) |
| image = | sobelZGradient3dImg (inImg,kernelType,bNormalize) |
Compute X, Y and Z gradients of an input image convolving it with 3d Sobel kernels.
3d Sobel kernels are separable, they can be decomposed as the product of 3 vectors. X gradient kernel equals to the product 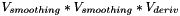 , Y gradient kernel equals to the product
, Y gradient kernel equals to the product 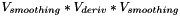 , and Z gradient kernel equals to the product
, and Z gradient kernel equals to the product 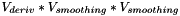 . Depending on the value of parameter
. Depending on the value of parameter 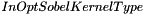 (default value: eSKT_SobelHalfKnlSz1), smoothing and derivative vectors equal to:
(default value: eSKT_SobelHalfKnlSz1), smoothing and derivative vectors equal to:
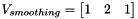 ,
, 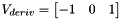 if
if 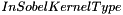 equals to eSKT_SobelHalfKnlSz1
equals to eSKT_SobelHalfKnlSz1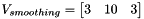 ,
, 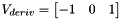 if
if  equals to eSKT_ScharrHalfKnlSz1
equals to eSKT_ScharrHalfKnlSz1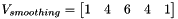 ,
,  if
if  equals to eSKT_SobelHalfKnlSz2
equals to eSKT_SobelHalfKnlSz2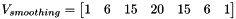 ,
, 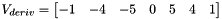 if
if 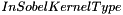 equals to eSKT_SobelHalfKnlSz3
equals to eSKT_SobelHalfKnlSz3
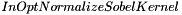 has the default value
has the default value 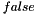 . When the user sets this parameter to the value
. When the user sets this parameter to the value 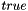 , only the smoothing part of the 2d kernel is normalized.
, only the smoothing part of the 2d kernel is normalized.
To handle image borders, a mirror extrapolation is used (see Border policy for more details).
Here is an example of a Sobel gradient applied to an 8-bits grey levels input image with default parameters used:
